บทนิยาม ฟังก์ชันที่มีโดเมนเป็นเซตของจำนวนเต็มบวกที่เรียงจากน้อยไปมากโดยเริ่มตั้งแต่ 1 เรียกว่า ลำดับ
ถ้าฟังก์ชันเป็นลำดับที่มีโดเมนเป็น { 1, 2, 3, …, n } เรียกว่า ลำดับจำกัด
และถ้าฟังก์ชันเป็นลำดับที่มีโดเมนเป็น { 1, 2, 3, … } เรียกว่า ลำดับอนันต์ 1. ความหมายของลำดับ
ในการเขียนลำดับ จะเขียนเฉพาะสมาชิกของเรนจ์เรียงกันไป
กล่าวคือ ถ้า a เป็น ลำดับจำกัด จะเขียนแทนด้วย a1, a2, a3, …, an
และ ถ้า a เป็น ลำดับอนันต์ จะเขียนแทนด้วย a1, a2, a3, …, an, …
เรียก a1 ว่า พจน์ที่ 1 ของลำดับ
เรียก a2 ว่า พจน์ที่ 2 ของลำดับ
เรียก a3 ว่า พจน์ที่ 3 ของลำดับ

และเรียก an ว่า พจน์ที่ n ของลำดับ หรือพจน์ทั่วไปของลำดับ
2. ตัวอย่างของลำดับ
a1 = 4 a2 = 7 a3 = 10 a4 = 13
และ an = 3n + 1
และ an = 3n + 1
2) – 2, 1, 6, 13, … เป็น ลำดับอนันต์ ที่มี
a1 = – 2 a2 = 1 a3 = 6 a4 = 13
และ an = n2 – 3
และ an = n2 – 3
การเขียนลำดับนอกจากจะเขียนโดยการแจงพจน์แล้ว อาจจะเขียนเฉพาะพจน์ที่ n หรือพจน์ทั่วไปพร้อมทั้งระบุสมาชิกในโดเมน
ตัวอย่าง
1) ลำดับ 4, 7, 10, 13 อาจเขียนแทนด้วย
an = 3n + 1 เมื่อ n  { 1, 2, 3, 4 }
{ 1, 2, 3, 4 }
 { 1, 2, 3, 4 }
{ 1, 2, 3, 4 } 2) ลำดับ – 2 , 1, 6, 13, … อาจเขียนแทนด้วย
an = n2 – 3 เมื่อ n เป็นจำนวนเต็มบวก
หมายเหตุ ในกรณีที่กำหนดลำดับโดยพจน์ที่ n หรือพจน์ทั่วไป ถ้าไม่ได้ระบุสมาชิกในโดเมน
ให้ถือว่าลำดับนั้นเป็น ลำดับอนันต์
3. ตัวอย่าง ลำดับต่อไปนี้เป็นลำดับจำกัด หรือ ลำดับอนันต์

ลำดับจำกัด เป็นลำดับที่มีโดเมนเป็นเซตของจำนวนเต็มบวก n พจน์แรก
ลำดับอนันต์ เป็นลำดับที่มีโดเมนเป็นเซตของจำนวนเต็มบวก
1) 6, 12, 18, 24, 30 เป็นลำดับจำกัด
2) 2, 4, 8, 16, …,  , … เป็นลำดับอนันต์
, … เป็นลำดับอนันต์
 , … เป็นลำดับอนันต์
, … เป็นลำดับอนันต์3) an = 5n – 2 เมื่อ n  { 1, 2, 3, …, 20 } เป็นลำดับจำกัด
{ 1, 2, 3, …, 20 } เป็นลำดับจำกัด
 { 1, 2, 3, …, 20 } เป็นลำดับจำกัด
{ 1, 2, 3, …, 20 } เป็นลำดับจำกัด4)  เป็นลำดับอนันต์
เป็นลำดับอนันต์
5) an = n2 + 3 เป็นลำดับอนันต์
ลำดับเรขาคณิต
บทนิยาม ลำดับเรขาคณิต คือ ลำดับที่มีอัตราส่วนของพจน์ที่ n+1 ต่อพจน์ที่ n เป็นค่าคงที่ ทุกค่าของจำนวนนับ n และเรียกค่าคงที่นี้ว่า “ อัตราส่วนร่วม ”
ถ้า a1, a2, a3, …, an, an+1 เป็นลำดับเรขาคณิต แล้ว จะได้
ตัวอย่าง ลำดับเรขาคณิต

ลำดับเลขคณิต
บทนิยาม ลำดับเลขคณิต คือ ลำดับที่มีผลต่างที่ได้จากการนำพจน์ที่ n+1 ลบด้วยพจน์ที่ n แล้วมีค่าคงที่เสมอ และเรียกผลต่างที่มีค่าคงที่ว่า ผลต่างร่วม ( Common difference )
ถ้า a1, a2, a3, …, an, an+1 , … เป็นลำดับเลขคณิต แล้ว
จะได้ a2 – a1 = a3 – a2 = … = an+1 – an เท่ากับ ค่าคงที่
เรียกค่าคงที่นี้ว่า “ ผลต่างร่วม ” (Common difference) เขียนแทนด้วย “ d ”
จากบทนิยาม d = an+1 – an








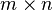 เราเรียกจำนวน
เราเรียกจำนวน  เพื่อหมายถึง เมทริกซ์
เพื่อหมายถึง เมทริกซ์ 

 เป็นเมทริกซ์ที่มีขนาดเท่ากันสองเมทริกซ์ เราสามารถนิยาม ผลรวม หรือ ผลบวก
เป็นเมทริกซ์ที่มีขนาดเท่ากันสองเมทริกซ์ เราสามารถนิยาม ผลรวม หรือ ผลบวก 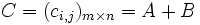 แล้ว
แล้ว 
 แล้ว
แล้ว 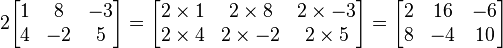
 เป็นเมทริกซ์สองเมทริกซ์โดยที่จำนวนหลักของ
เป็นเมทริกซ์สองเมทริกซ์โดยที่จำนวนหลักของ 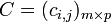 โดยที่
โดยที่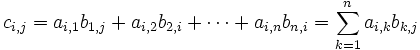
 เป็นเวกเตอร์ที่มีสมาชิกเป็นสมาชิกในแถว
เป็นเวกเตอร์ที่มีสมาชิกเป็นสมาชิกในแถว  เป็นเวกเตอร์ที่มีสมาชิกเป็นสมาชิกในหลัก
เป็นเวกเตอร์ที่มีสมาชิกเป็นสมาชิกในหลัก  เมื่อ
เมื่อ  คือ
คือ


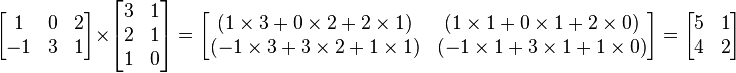
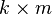 ,
,  ใดๆ ("สมบัติการเปลี่ยนหมู่")
ใดๆ ("สมบัติการเปลี่ยนหมู่") แล้ว ผลคูณ
แล้ว ผลคูณ  แล้ว
แล้ว  ส่วน
ส่วน  ผลคูณทั้งสองจึงมีค่าไม่เท่ากันอย่างเห็นได้ชัด
ผลคูณทั้งสองจึงมีค่าไม่เท่ากันอย่างเห็นได้ชัด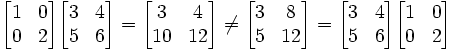



 หรือ
หรือ  หรือ
หรือ  หรือเขียนแทนด้วยการสลับเปลี่ยนสังยุคของเมทริกซ์ จะได้ว่า
หรือเขียนแทนด้วยการสลับเปลี่ยนสังยุคของเมทริกซ์ จะได้ว่า 

